Buoyancy

Physical properties

Visualisation

About this simulation

This is an approximate model of the upthrust (buoyancy) and drag on a sphere in a fluid.
The upthrust is simply equal to the weight of the displaced fluid: 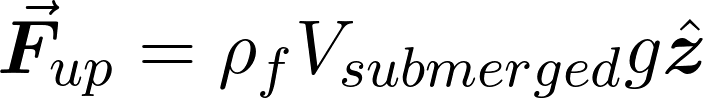where the subscript f refers to the fluid, and V is the volume of the sphere which is submerged. By comparing this with the weight of the sphere, you can conclude that objects sink if they are more dense than the fluid they are in, and float if they are less dense.

The drag is in theory much more complicated, as for an accurate model, one would need to account for the profile of the object and the turbulence of the fluid flow, among other things. For the sake of simplicity, I opted for Stokes' drag alongside the drag equation. 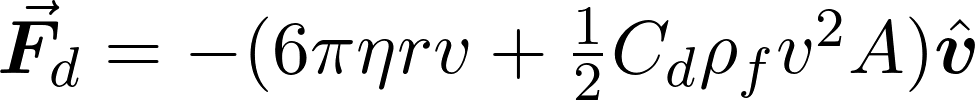The first term in this equation for the drag force is the Stokes' drag, which depends on the viscosity of the fluid. It assumes a spherical object (perfect for this case) and very small Reynolds numbers, which implies next to no turbulence in the fluid. These assumptions result in this very simple expression for the viscous drag on a sphere.
The second term is the drag equation, and depends on the profile (i.e. size, shape and inclination) of the object. Here, the shape of the object (in this case a sphere) is accounted for in the drag coefficient, C_d, and its size is represented by the area A. As you would imagine, more aerodynamic objects such as the wing of an aeroplane have a small coefficient, while objects such as this sphere have a larger one and experiece more drag as a result. In reality, the drag coefficient varies with the Reynolds number of the fluid, but I won't talk about this here. Notice that the drag equation term is proportional to the square of velocity, while the Stokes' drag is linear in velocity.
Of course, both of these drag forces act in the opposite direction to the velocity, v of the object, hence the minus sign and proportionality to the object's velocity.